
Abstract
We present locoGP, a Genetic Programming (GP) system written in Java for evolving Java source code. locoGP was designed to improve the performance of programs as measured in the number of operations executed. Variable test cases are used to maintain functional correctness during evolution. The operation of locoGP is demonstrated on a number of typically constructed “off-the-shelf” hand-written implementations of sort and prefix-code programs. locoGP was able to find improvement opportunities in all test problems.
This paper introduces locoGP1, a Genetic Programming (GP) [14] system written in Java for improving program performance using a Java source code representation2. As Java is a widely used general purpose language, the ability to automatically improve existing Java programs is of wide interest. In this context, GP is a good approach for exploring the implicit effects of source code changes on performance [42, 17].
Evolving code in a general language is a challenge due to the broad range of constructs that form such languages. A self-contained GP system, such as tinyGP [29], includes its own language (as defined by the primitives chosen), parser and interpreter. Interpretation and evaluation of programs can be achieved in a small amount of code by choosing a set of primitive functions specifically for a problem. Fortunately, there exist comprehensive libraries for parsing, compiling and interpreting more general Java programs upon which locoGP relies heavily.
In locoGP, the primitive set is defined by Java language elements which exist in the program to be improved and may include statements, expressions, variable names or operators. Source code is modified in an Abstract Syntax Tree (AST) representation which specifies the typing of nodes and structure of a program in the Java language.
Performance is measured by counting the number of instructions taken to execute a program. Program results are measured for correctness with a problem-specific function by counting functionality errors. Fitness is measured by normalising and combining performance and functionality error measures in a weighted sum. Selection favours minimising the execution count and functionality error in a program.
This paper extends previous work [6] by discussing locoGP in detail and presenting results of its operation on a number of sort and prefix code problems. A performance improvement was found in all problems. locoGP can be readily extended to further Java improvement problems or used as a comparison point with other code improvement systems.
This paper is organised as follows. In the following section we present related work. The mechanisms and configuration used in locoGP are covered in Section 3. The amount and type of improvement found in a number of test problems is shown in Section 4. The paper is concluded in Section 5 with future work.
Various languages have been used to evolve programs with GP. The choice of programming language and the goal of evolution (improvement in this case) impacts how GP can be applied.
GP has generally been used to evolve S-expressions and programs in specialised languages [35]. Programs are frequently restricted to domain specific language primitives (for example, the use of a swap function in sort [12, 24] or subsets of primitives from general purpose languages [41]. Many GP systems include their own parsers and interpreters. However, a wide range of programs are written in general-purpose imperative languages such as Java and so recent work has turned to improving such programs [37, 26, 2, 3].
As the language used becomes more complex, so too does the infrastructure needed to modify and evaluate programs. As general purpose languages have non-trivial syntax and semantics, code may be translated or compiled to a different representation for various purposes. To mitigate the cost of program evaluation, programs can be compiled [9]. Additionally, an intermediate representation has been used for modification before a program is compiled where the semantics of a language are particularly nuanced, as is the case with C [22]. Java bytecode is a relatively high-level representation which can be translated into more readable Java code after evolution [25].
Although programs can be modified in a range of languages, there is a further representation choice that can be made when considering how code is to be modified. Code can be modified with single edits to language-level elements. Multiple elements can be changed where a single modification changes a line of code [38], a statement as defined by the language [18] or as prescribed by a design pattern [23].
When improving existing programs, the language, primitives, representation and modification mechanisms are chosen in response to available code. As we are dealing with existing code, GP is “seeded” with a program which is modified to produce variants [2]. Improving existing programs infers a large amount of code reuse where primitives and genetic material are generally gleaned from the seed program under improvement. Primitives are still hand-crafted and domain specific in some sense as the original program was constructed for a particular purpose. Primitives are not, however, created by the GP practitioner specifically to aid evolution.
During GP, the majority of modifications to a seed program are highly likely to produce degraded variants. It may not be possible to evaluate a large percentage of the programs created during random modification as they may not compile or may contain infinite loops [32]. When programs do not compile, they are typically discarded [37, 27]. Among program variants that do compile, the seed is likely to have relatively high fitness and represents a local optima in the population.
To ensure the best fitness in each generation does not drop, elitism promotes the best programs from the previous generation to the next. A percentage of the worst programs in the next generation can be replaced by the best of the previous. As program modification is highly destructive, elitism rates used for program improvement tend to be high. Up to 50% of programs may be removed [8], though this approach uses “crossing back” between each remaining program and the original program to create the next generation instead of using more standard elitism.
In GP, it is important to capture the characteristics of a desired solution to ensure evolutionary pressure is towards the desired goals. Designing a fitness function which gives a scale for how good a program is, can be non-trivial particularly when the scale relates to functionality [12]. The issue lies in measuring program functionality in order of increasing utility. In a sorting example, a program which swaps two identical values in a list would be considered better than a program which does not change the list at all even though the fitness remains the same. If a desired trait cannot be measured, or receives a value lower than it should, then GP will not promote its use in the population.
To maintain correctness, a graduated functionality metric can be created by summing the results of binary test cases as part of the fitness function [2, 21]. The seed program can be used as an oracle [19] when given various test input data. Binary test cases as used in Software Engineering (SE) are distinct from the traditional use of a fitness functions in GP. In SE, each test case returns a Boolean value. In GP the correctness of a single result is calculated along a variable scale.
Measuring performance introduces parsimony pressure to the search process resulting in less costly programs, mitigating the issue of bloat somewhat [34]. How performance is measured focuses evolutionary pressure toward finding different improvements. Performance and even functionality gains can be achieved by specialising code for a particular input data type [19] or distribution [2]. A more general representative set of input data can be expected to find only general algorithmic improvement.
Program execution performance can be measured as wall clock time, number of CPU cycles taken, number of method calls, number of lines executed or even as the energy consumption of the application.
Wall clock time may be the most far reaching as it measures the length of time a program takes to complete regardless of how much memory, network, CPU or energy is used during execution. Therefore a code improvement in any of these areas can be detected and promoted. Measuring all of these traits in one metric introduces wide variability every time the same program is executed with the same input data as the execution environment is difficult to control. Network, CPU or virtual machine scheduling can add variability [16]. Evaluation can be repeated to reduce the measurement noise but is expensive. Where the measurement signal is larger than any noise, wall clock time is particularly useful [4]. Estimates of execution cost can also be used to evolve programs with respect to power consumption [42].
Ignoring environment specific measures gives a deterministic measure. Such measures include counting the number of lines of code [18] and instructions executed [15].
| Approach | Representation | Improvement | Fitness Metric |
| locoGP | Java (AST) | Performance | Bytecode Operations |
| Langdon [17], Petke [28] | C++ (Statement) | Performance, Specialisation | Line Count |
| Arcuri [2], White [41] | Java-like (AST) | Performance | Simulated CPU Cycle |
| Walsh & Ryan (Paragen) [31, 30], | Parallelisation Instructions | Parallel Programs | Functionality |
| Chennupati (MCGE) [4] | |||
| Orlov (FINCH) [25] | Java (Byecode) | Functionality | Error Count |
| Castle [3] | Java-like (AST) | Functionality | Error Count |
| O’Cinnéide [5], Simons [33] | Java (Refactoring Patterns) | Quality (e.g. elegance) | Software Metrics |
locoGP utilises many of the mechanisms from the related work such as seeding and modification at the language level. The main distinction between the related work and locoGP is the use of Java source code. locoGP is seeded with compilable and fully functional source code which is modified at the Java language level. A summary comparison between locoGP and other notable improvement systems can be seen in Table 13.
An initial population of individuals is generated by taking the program to be evolved as the seed individual and mutating it. As the seed program represents a local optima, and is likely to be the most fit program for a number of the initial generations during GP, we seek to encourage diversity in the population. If we do not encourage diversity, we may end up with a population where the majority of programs are very similar to the seed. New generations of individuals are created by the application of mutation (30%) and crossover (90%) operators as described in Section 3.2.
A gentle selection pressure (tournament of two) and aggressive mutation rate (30%) is chosen. Modifying programs in Java is highly likely to produce disfunctional or even non-compilable programs. Programs are in competition with an already functioning seed program. We end up with many programs which are close to the seed due to selection, and many programs which have very poor fitness due to destructive modifications. To balance out the distribution of programs along the fitness scale, we use elitism which selects a small number of programs at each fitness value and replaces the worst 30% of programs with these.
locoGP performs the cycle of parsing, compilation, instrumentation and execution of programs in memory with results written to disk periodically. locoGP relies on the freely available and widely popular Eclipse Java Development Tools (JDT) for parsing programs to an AST representation. The JDT provides methods for cloning, traversing and modifying program trees and is also used to gather statements, expressions and variables from a program which can then be modified as per the GP operators.
Primitives are drawn from those that exist within the program to be improved. Node selection is not uniform in an AST as each node is not represented in the same way within an AST. For example, operators do not exist as nodes in an AST but are attributes of expression nodes. An AST gives us a representation devoid of source code artifacts such as parentheses and line terminators. Depending on the node type chosen, the operation performed may be different.
When creating a new individual, a parent program is chosen using tournament selection. A clone is made of the selected program using the JDT and the new program is then modified using mutation, or crossover with another parent program (requiring an additional tournament). For each crossover or mutation operator application, only one offspring individual program is generated.
The Java language syntax is enforced by the AST and is used to restrict node compatibility. Where a node such as an expression is chosen, it is possible that the node can be replaced with another expression or a variable name. Where a statement is selected, it may be replaced by another statement, or statement sub-type such as an IF or WHILE statement. A replacement node can be a whole sub-tree, e.g. in the case of a statement replacement. In this case, the node which is the root of the sub-tree is of concern. If we pick a block, we clone some other random line of code as an addition to the block.
While typing prevents some invalid code replacement, such as replacing an operator with a variable, the AST can nonetheless be modified to produce syntactically incorrect programs which do not compile. Due to this, the number of discarded programs created due to compilation errors is relatively high.
Crossover and mutation operators are used to modify code as per AST typing. We pick a node and then decide what to do with it depending on what is possible. Once a node is selected, it and the whole AST sub-tree is subject to replacement, deletion or cloning, depending on node and GP operator. It is also possible for two code edits to be made where crossover and mutation are both applied in creating a new program.
Two parent programs are required for crossover to be applied. The subtree at a randomly selected node in the first program is replaced with the clone of a subtree of an allowed type from the second program. Crossover only allows the exchange of statement and expression node types (both infer sub-tree replacement) between two programs. Leaf nodes may not be involved in this process as the modification of a single element in a program is handled by mutation. Crossover is repeatedly attempted until a compilable program is produced, or a maximum of 100 attempts have been made. After 100 attempts, a different pair of parent programs are selected using tournaments.
Mutation involves applying change to a single individual program in the form of cloning, deletion or replacement of randomly selected nodes. It is used exclusively to generate the initial population of programs and in conjunction with crossover for subsequent generations. How mutation is performed is dependent on the node that is selected within an individual. If the node is a block statement, then a statement is inserted, with no choice for deletion or modification of the contents of the block. If the node is a particular expression, such as infix or postfix, then the operator is changed for a different one. If the node is a statement, its contents may be modified or the statement can be deleted. If the node is of another type, such as variable, then it can only be replaced and deletion is not an option due to syntax constraints.
| Parameter | Value |
| Representation | Java AST |
| Operators | Crossover, Mutation |
| Crossover Rate | 0.9 |
| Mutation Rate | 0.3 |
| Individual Selection | Tournament (2) (read text) |
| Initialisation Method | Mutated Seed |
| Max Operator Application | 100 |
| Population Size | 250 |
| Generations | 100 |
| Elitism | 30% of unique fittest |
After modification, the modified AST representation is converted back to source code text and compiled to bytecode. The resulting bytecode is instrumented using a bytecode counting library [15]. Instrumentation adds extra code to the program to count the number of bytecodes that are executed when the code is run.
We measure code operations executed specifically by counting bytecode executed in Java [15]4.
The evaluation mechanism, and how performance is measured affects the type of program improvement that is likely to be found. Measuring operations performed ignores platform specific differences in performance, and means the GP algorithm differentiates programs only on their ability to reduce execution count. This is expected to promote search for general code improvements. Counting bytecodes executed gives a measure which does not vary between runs, and can be expected to be portable.
When executed, bytecode may contain infinite loops and so execution is restricted by a timeout period [39], after which programs are halted.
The bytecode is executed numerous times with a range of input data and the returned values are compared with known correct values. Results are tested for correctness error against the results obtained from executing the seed program. Our measure of correctness error is not binary, but graduated. A problem-specific fitness function is used in conjunction with the seed program acting as oracle. While we can use a general measure for performance, functionality measures are problem specific and are discussed further alongside the problems we use in Section 4.1.
Assuming a program halts within the timeout period, counting and test case results can be collected. Programs which compile and execute, but exhibit runtime errors or do not finish within the time bounds are given the worst fitness values possible so that elitism or selection can discard them.
Both performance and functionality measures are normalised against the seed program. Execution count of a variant program is divided by the execution count of the seed program. If the performance is the same as the seed, a normalised performance value of one results. The summed error count from all test cases is subtracted from the error count value for the seed program and divided by the seed error count (Eq. 1). If a program is considered correct, evaluation will give a value of zero for functionality error.
 | (1) |
The fitness function is a weighted sum of performance and 100 times the functionality error as shown in Eq. 2.
The weighting of 100 allows semi-functional programs to be “binned” or grouped roughly by their functionality. Two correct programs (or programs which score the same functionality error) are then distinguished by performance values only. A correct program having the same performance as the seed will receive a fitness of one. Programs which use fewer operations will receive a value less than 1.
As selection favours smaller fitness values, we are minimising the number of operations executed when a program is run as well as the functionality error. Thus, there is a built-in parsimony pressure [34] towards programs which are no longer than they need to be to provide the desired functionality. Where a program is functionally correct, any additional code executed reduces the fitness value. This parsimony pressure means that programs do not grow too long in size as superfluous code is removed and bloat is not a major issue in locoGP.
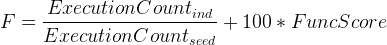 | (2) |
We use a form of elitism at the rate of 30% which we term “diverse elitism”. When gathering the elite programs from the previous generation, we truncate the decimal part of fitness values. We then take a program from the top 30% unique fitness values. Ignoring the decimal place means we are largely ignoring performance, and only distinguishing on functionality for the most part. For each whole number fitness value, we select only one program. The effect of this is that we do not select similar programs which have the same functionality. The worst 30% of the new generation is selected (ignoring diversity) and is replaced by these elite programs.
We experiment with locoGP on a number of sort algorithms and a Huffman codebook generating algorithm.
The sort implementations were taken mostly unmodified or “off-the-shelf” from online sources [36]. An implementation of prefix codebook generation as used during Huffman coding [11] was written to include one of our sort algorithms as a sub-function. Our “prefix codebook” problem entails finding the set of shortest codewords where no code forms a prefix of another. The algorithm is passed an array of characters where each character is represented by a fixed number of bits. The algorithm is expected to return a codebook of character to codeword mappings, where frequently used characters are represented by codewords of fewer bits. The bubblesort algorithm is embedded in the candidate solution as we are familiar with the improvements which exist. The Huffman codebook problem, although incorporating bubblesort (and in turn the same improvement opportunities), has a different fitness function, larger seed program size, and is broken into a number of classes.
These programs consist of common algorithms that are well studied, have many versions with reasonable interest in their improvement. The problems are relatively small, but their size is large enough that we can assume GP is unlikely to generate these programs from scratch without being given domain specific primitives [1]. They are big enough to pose as difficult problems for GP to improve, but small enough that any improvements may be understood.
Measuring functionality at a detailed level is not trivial and requires careful consideration to get functionality improvements in order of importance [12].
For a sort algorithm, we construct a measure for how “sorted” a list of numbers is by counting how far each number is away from where it should be in a correctly sorted list. This is calculated by summing up “errors” in placement of values in a list. If a value is in the right location, the error count is incremented by one. If the value is not in its correct place but has been moved then error count is incremented by two. If the value has not moved at all, then error count is incremented by three. This approach measures when a value does not move and allocates the highest error value. At least when a value has been moved, albeit to the wrong place, the program is exhibiting functionality which is more desirable than not moving the value at all. A number of fixed test arrays are used to inspect variant sort programs. Each test array consists of a list of integers. The sort algorithm in the Java library is used as an oracle to check correct answers.
For the prefix codebook problem, we have written a function which checks if the result returned is a valid set of prefix codes. Test arrays of characters are used. A prefix codebook should have the same number of codes as there are different characters in the input data. If the number of codewords returned is incorrect, we count the number of extra or missing codes and add them to the error. We count the number of prefix violations and add them to the error count. A prefix violation occurs when a codeword forms the prefix of any other codeword. As the goal of prefix code algorithms is to reduce the overall length of valid codewords for a particular input, we sum the length of each codeword and add this to the error.
If either a codebook length or prefix violation error is found, the error count is further penalised by the extra addition of the length of all codewords in the oracle codebook answer. As codebook length and prefix violations may be small, we must ensure that a program which has either of these errors does not get a better score than the oracle answer. If a single prefix error is detected, the value of one may be added to the error, even though the codeword length is smaller than the oracle answer. Without penalising such cases, a program with prefix errors would appear better than a correct oracle answer. Multiple test values are used in both cases of sort and prefix codes. The error count from each test is summed as overall functionality error count.
To introduce locoGP and characterise its operation, we initially focus on a single run on a bubblesort implementation and then show results across a number of sort and prefix code programs.
Figure 1 shows a scatter plot of fitness values for all individuals in each generation and the average fitness per generation of a typical GP run on bubblesort. Each dot in the graph is the fitness of a single individual program. The line shows the average fitness of each generation.
The fittest individuals from each generation can be seen as the lowest dots in Figure 1. By following the lowest values, we can see a single distinct improvement to 0.6 at generation 57. This represents a saving of 40% of the execution cost of this algorithm in terms of bytecode’s executed (note this does not necessarily equate to 40% wall-clock time saving).
As indicated in Section 3, the first generation is created with mutation only. When starting GP from a correct seed program, fitness improvements are rare. Due to the representation and operators, it is highly unlikely that the seed program will be improved upon when initially modified. The assumption being that the seed is some local optima which must be escaped before an improvement can be made. Most changes to the seed will degrade the fitness, especially when using programming languages which have complicated syntax and semantics. Thus the program must in some sense be “broken” before it can be improved.
In generations subsequent to the first, programs are created with crossover and mutation. The average fitness line in 1 shows the average population fitness deteriorates (moves higher in the graph) in initial generations. Elitism favours better programs which become more numerous in subsequent generations. In later generations, there is a greater chance that a new individual will have a better fitness, which can be seen as the dots lower than fitness one in the graph.
Of note is the modality of the distribution of fitness values in each generation. Fitness distribution in each generation is multi-modal due to the weighted sum fitness function and semantics of the particular implementation under improvement. Even though the actual fitness values of variant programs are somewhat arbitrary under random modification, it is curious to consider that the language semantics, program code and operations of GP result in some program variants being created in abundance which cluster at certain fitness values. Few individuals evaluate to some regions of the fitness gradient. This can be seen in the grouping of indvidual fitness values into rows on the graph. This may be because our multiplication of 100 of the functionality provides spacing between functionality levels which the performance variability is not large enough to fill in the gap between functionality “levels”. Although the tournament size of 2 we use is a light pressure on the population fitness, the elitism rate of 30% is more aggressive and this can be seen as the algorithm progresses where the worst individuals are being replaced faster than they are being created.
Applying GP to software improvement provides a graph showing few fitness improvements to the seed. More tradtional applications of GP, which are used to “grow” a solution program outright, are more likely to show a graph with a smoother curve of many improvements in fitness. GP on existing fully-functional programs is starting from a local optima and is attempting to find one of very few improvements. The overall shape of the graph shows the scale of the problem, and the jaggedness of the search space, where a smooth gradient of program improvement is not likely. Visually, the best individual programs (i.e. the lowest dots in each generation) in 1 show a straight line at value one, until generation 57 where fitness improves to 0.6.
Considering that improvements in fitness are rare, it may unfortunately appear that improved programs are found more or less at random, and the genetic nature of the GP algorithm does not give it much advantage over random search for the problem of program improvement. Although there is the temptation to classify this search process as being more “random” than it is “genetic”, GP on subsequent problems shows that genetic operators are advantageous for delivering even a single fitness improvement. Even though there may be no fitness improvement on the seed observed, the search process is busy exploring lineages of programs which are necessary to reach an improved variant.
| Problem Name | AST Nodes | Improvement Nodes | LOC | Best Fitness | % Discarded |
| Insertion Sort | 60 | 3 | 13 | 0.91 | 73.3 |
| Bubblesort | 62 | 5 | 13 | 0.55 | 71.4 |
| BubbleLoops | 72 | 8 | 14 | 0.29 | 71.8 |
| Selection Sort 2 | 72 | 1 | 16 | 0.99 | 70.9 |
| Selection Sort | 73 | 1 | 18 | 0.98 | 71.2 |
| Shell Sort | 85 | 3 | 23 | 0.95 | 71.4 |
| Radix Sort | 100 | 3 | 23 | 0.99 | 80.5 |
| Quick Sort | 116 | 2 | 31 | 0.46 | 72.7 |
| Cocktail Sort | 126 | 1 | 30 | 0.85 | 73.7 |
| Merge Sort | 216 | 1 | 51 | 0.95 | 73.2 |
| Heap Sort | 246 | 2 | 62 | 0.59 | 71.1 |
| Huffman Codebook | 411 | 5 | 115 | 0.57 | 83.8 |
An improved version of each program was found for all of the programs tested as can be seen in Table 3. We can say that for these common algorithm implementations, GP can find a modification which reduces execution count.
A count of the AST nodes available for modification in each program shows the number of modification points which can be chosen during the application of GP. Lines of code are counted including those containing braces [40]. The number of discarded programs is a ratio of the number of programs which do not make it into each generation over the total number of programs produced. Discarded programs include those which do not compile and intermediate programs generated where mutation and crossover are applied together. This is different to software mutational robustness [32] which measures the number of modifications which leave a program’s behaviour unchanged. In our experiments, a minuscule number of programs, certainly less than 1%, show no behavioural change when modified. This may be due to programs likely containing only code which has some function.
The improvements found are in some cases reduction in number of iterations through a loop. The number of nodes which must change to produce an improved variant of the program is relatively small. In improved programs across these problems we see both the reuse of existing code and the modification of code at a fine level, justifying the use of the “genetic” as well as mutational approach of GP. To improve some programs, only a small number of edits are required. On others, it is necessary for a “block” of code to be reused and subsequently modified to produce a variant program. In either case, a strict or rigid definition of a building block may be overly restrictive. If a building block preserving GP extension were to be used, it would have to allow the modification of the contents of a building block after it has been defined.
There is an opportunity for improvement in existing code as our results have shown. If improvements can be found in such relatively small algorithms, we may speculate that it is likely that there is a greater number of improvement opportunities in larger programs. We feel improvement opportunities exists in the wider body of existing code, especially considering that performance is not frequently recommended as of primary importance when developing software [13].
Depending on the language that programs are to be evolved in, the tools for manipulating the language may not be readily available. One example is C which, due to the historical variety of versions implemented, can be difficult to parse in all instances [22]. As such, we feel it is important to currently focus on infrastructure to enable program improvement. locoGP can be used as a proof-of-concept in this regard.
Though relatively expensive, compiling Java source code for evaluation during evolution is manageable on modern hardware. There is ample room for improvement of locoGP itself both in terms of implementation5 and in terms of the GP configuration used. Bytecodes could be weigthed differently as they are being counted as per their type or by their execution context. Performance could also be measured as wall-clock time to capture overhead introduced during I/O operations. Code exists in locoGP for measuring wall-clock time though was only used in early experiments as gathering consistent measures required repeat program execution which slowed the GP algorithm. The GP configuration used could be extended with tabu-search-like improvements [7] such as restricting the generation of equivalent programs [18] or caching previous evaluation results would reduce the cost of the system. A steady-state GP algorithm with different elitism or distribution models may also improve the operation of locoGP.
Additional sort and prefix code problems can be added to locoGP with minimal effort. Improving additional problems (other than sort and prefix codebook) requires writing a functionality measure and adding relevant test data. locoGP can be used as a comparison point between other systems which evolve programs at different represenations such as bytecode [25], statement [28, 41] and/or patch [8, 18].
locoGP may be also used to observe issues in scaling automated software improvement to larger problems. A major theme in program improvement is the reuse of code, more specifically finding where [6, 18, 39]6 and with what [10, 20] a program should be modified with.
We thank the anonymous reviewer for suggesting the weighting of different bytecodes and I/O considerations. Edgar Galván López’s research is funded by an ELEVATE Fellowship, the Irish Research Council’s Career Development Fellowship co-funded by Marie Curie Actions. The second author would also like to thank the TAO group at INRIA Saclay & LRI - Univ. Paris-Sud and CNRS, Orsay, France for hosting him during the outgoing phase of the ELEVATE Fellowship.
[1] Agapitos, A., and Lucas, S. Evolving modular recursive sorting algorithms. Genetic Programming (2007), 301–310.
[2] Arcuri, A., White, D., Clark, J., and Yao, X. Multi-objective improvement of software using co-evolution and smart seeding. Simulated Evolution and Learning (2008), 61–70.
[3] Castle, T., and Johnson, C. G. Evolving high-level imperative program trees with strongly formed genetic programming. In Genetic Programming. Springer, 2012, pp. 1–12.
[4] Chennupati, G., Azad, R. M. A., and Ryan, C. Automatic evolution of parallel sorting programs on multi-cores. In Applications of Evolutionary Computation. Springer, 2015, pp. 706–717.
[5] Cinnéide, M. O. Automated application of design patterns: a refactoring approach. PhD thesis, Trinity College Dublin., 2001.
[6] Cody-Kenny, B., and Barrett, S. The emergence of useful bias in self-focusing genetic programming for software optimisation. In Symposium on Search-Based Software Engineering (Leningrad, Aug. 24-26 2013), G. Fraser, Ed. Graduate Student Track.
[7] Díaz, E., Tuya, J., Blanco, R., and Dolado, J. J. A tabu search algorithm for structural software testing. Computers & Operations Research 35, 10 (2008), 3052–3072.
[8] Forrest, S., Nguyen, T., Weimer, W., and Goues, C. L. A genetic programming approach to automated software repair. In GECCO (2009), F. Rothlauf, Ed., ACM, pp. 947–954.
[9] Fukunaga, A., Stechert, A., and Mutz, D. A genome compiler for high performance genetic programming. Genetic Programming (1998), 86–94.
[10] Harman, M., Jia, Y., and Langdon, W. B. Babel pidgin: SBSE can grow and graft entirely new functionality into a real world system. In SSBSE Challenge Track (Fortaleza, Brazil, 26-29 Aug. 2014), M. Barros, Ed. Accepted.
[11] Huffman, D. A., et al. A method for the construction of minimum redundancy codes. Proceedings of the IRE 40, 9 (1952), 1098–1101.
[12] Kinnear Jr, K. Evolving a sort: Lessons in genetic programming. In Neural Networks, 1993., IEEE International Conference on (1993), IEEE, pp. 881–888.
[13] Knuth, D. E. Structured programming with go to statements. ACM Computing Surveys (CSUR) 6, 4 (1974), 261–301.
[14] Koza, J. R. Genetic programming: on the programming of computers by means of natural selection, vol. 1. MIT press, 1992.
[15] Kuperberg, M., Krogmann, M., and Reussner, R. ByCounter: Portable Runtime Counting of Bytecode Instructions and Method Invocations. In Proceedings of the 3rd International Workshop on Bytecode Semantics, Verification, Analysis and Transformation , Budapest, Hungary, 5th April 2008 (ETAPS 2008, 11th European Joint Conferences on Theory and Practice of Software) (2008).
[16] Lambert, J. M., and Power, J. F. Platform independent timing of java virtual machine bytecode instructions. Electronic Notes in Theoretical Computer Science 220, 3 (2008), 97–113.
[17] Langdon, W. Performance of genetic programming optimised bowtie2 on genome comparison and analytic testing (gcat) benchmarks.
[18] Langdon, W. B., and Harman, M. Genetically improving 50000 lines of C++. Research Note RN/12/09, Department of Computer Science, University College London, Gower Street, London WC1E 6BT, UK, 19 Sept. 2012.
[19] Langdon, W. B., and Harman, M. Optimising existing software with genetic programming. IEEE Transactions on Evolutionary Computation (2013).
[20] Le Goues, C., Dewey-Vogt, M., Forrest, S., and Weimer, W. A systematic study of automated program repair: Fixing 55 out of 105 bugs for $8 each. In Software Engineering (ICSE), 2012 34th International Conference on (2012), IEEE, pp. 3–13.
[21] Le Goues, C., Weimer, W., and Forrest, S. Representations and operators for improving evolutionary software repair. In Proceedings of the fourteenth international conference on Genetic and evolutionary computation conference (2012), ACM, pp. 959–966.
[22] Necula, G. C., McPeak, S., Rahul, S. P., and Weimer, W. Cil: Intermediate language and tools for analysis and transformation of c programs. In Compiler Construction. Springer, 2002, pp. 213–228.
[23] O’Keeffe, M., and Cinnéide, M. Search-based refactoring: an empirical study. Journal of Software Maintenance and Evolution: Research and Practice 20, 5 (2008), 345–364.
[24] O’Neill, M., Nicolau, M., and Agapitos, A. Experiments in program synthesis with grammatical evolution: A focus on integer sorting. In Evolutionary Computation (CEC), 2014 IEEE Congress on (2014), IEEE, pp. 1504–1511.
[25] Orlov, M., and Sipper, M. Flight of the finch through the java wilderness. Evolutionary Computation, IEEE Transactions on 15, 2 (2011), 166–182.
[26] Petke, J., Harman, M., Langdon, W. B., and Weimer, W. Using genetic improvement & code transplants to specialise a c++ program to a problem class. In 17th European Conference on Genetic Programming (EuroGP), Granada, Spain (2014).
[27] Petke, J., Langdon, W. B., and Harman, M. Applying genetic improvement to minisat. In Search Based Software Engineering. Springer, 2013, pp. 257–262.
[28] Petke, J., Langdon, W. B., and Harman, M. Applying genetic improvement to MiniSAT. In Symposium on Search-Based Software Engineering (Leningrad, Aug. 24-26 2013), G. Fraser, Ed. Short Papers.
[29] Poli, R. TinyGP. http://cswww.essex.ac.uk/staff/rpoli/TinyGP/, 2004.
[30] Ryan, C. Automatic Re-engineering of Software Using Genetic Programming, vol. 2 of Genetic Programming. Kluwer Academic Publishers, 1 Nov. 1999.
[31] Ryan, C., and Walsh, P. Paragen ii: evolving parallel transformation rules. In Computational Intelligence Theory and Applications. Springer, 1997, pp. 573–573.
[32] Schulte, E., Fry, Z. P., Fast, E., Weimer, W., and Forrest, S. Software mutational robustness. arXiv preprint arXiv:1204.4224 (2012).
[33] Simons, C. Interactive evolutionary computing in early lifecycle software engineering design.
[34] Soule, T., and Foster, J. A. Effects of code growth and parsimony pressure on populations in genetic programming. Evolutionary Computation 6, 4 (1998), 293–309.
[35] Spector, L. Autoconstructive evolution: Push, pushgp, and pushpop. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2001) (2001), pp. 137–146.
[36] Various. Rosettacode.org. http://rosettacode.org. Accessed: 2014-09-30.
[37] Weimer, W., Forrest, S., Goues, C. L., and Nguyen, T. Automatic program repair with evolutionary computation. Commun. ACM 53, 5 (2010), 109–116.
[38] Weimer, W., Nguyen, T., Goues, C. L., and Forrest, S. Automatically finding patches using genetic programming. In ICSE (2009), IEEE, pp. 364–374.
[39] Weimer, W., Nguyen, T., Le Goues, C., and Forrest, S. Automatically finding patches using genetic programming. In Proceedings of the 31st International Conference on Software Engineering (2009), IEEE Computer Society, pp. 364–374.
[40] Wheeler, D. A. Sloccount, 2001.
[41] White, D., Arcuri, A., and Clark, J. Evolutionary improvement of programs. Evolutionary Computation, IEEE Transactions on, 99 (2011), 1–24.
[42] White, D. R., Clark, J., Jacob, J., and Poulding, S. M. Searching for resource-efficient programs: Low-power pseudorandom number generators. In Proceedings of the 10th annual conference on Genetic and evolutionary computation (2008), ACM, pp. 1775–1782.
1The name locoGP originated from early experimentation with lines of code and objects but is of little significance in the context of the current locoGP implementation.
2Source code of locoGP and problem set are available from the first author.
3Systems specifically for bug-fixing are not included.
4Source code is available from the authors of bycounter which is a dependency of locoGP.
5The notion of using locoGP to improve locoGP poses an enticing challenge.
6locoGP also implements mechanisms for node selection bias within a program as an experimental feature.